函数与导数中常用的函数和不等关系
前言
高考中在压轴题中考查的函数有千千万,但是总能从其中找到一些比较核心的函数来;
\(e^x\geqslant ex\) , \(\cfrac{1}{e}x\geqslant \ln x\) ,
常用函数
比如基本初等函数\(f(x)=x\)和\(g(x)=e^x\)做四则运算得到的这些函数:
\(h(x)=x\pm e^x\);

\(m(x)=x\cdot e^x\);\(n(x)=\cfrac{e^x}{x}\);\(r(n)=\cfrac{x}{e^x}\);
分析:若熟知上图的图像,分离参数,数形结合可得正确选项为\(D\)。

比如基本初等函数\(f(x)=x\)和\(g(x)=\ln x\)做四则运算得到的这些函数:
\(h(x)=x\pm \ln x\);
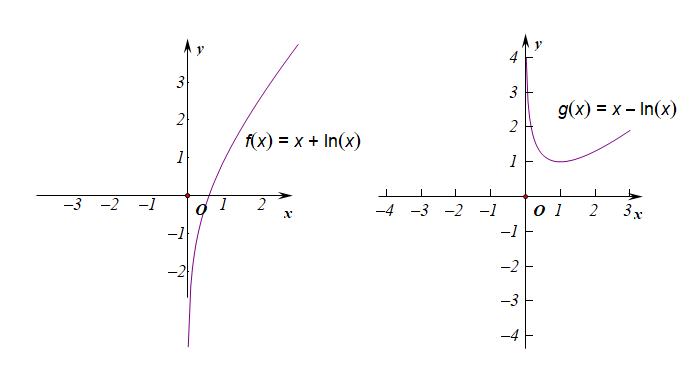
\(h(x)=x\cdot \ln x\);\(h(x)=\cfrac{\ln x}{x}\);
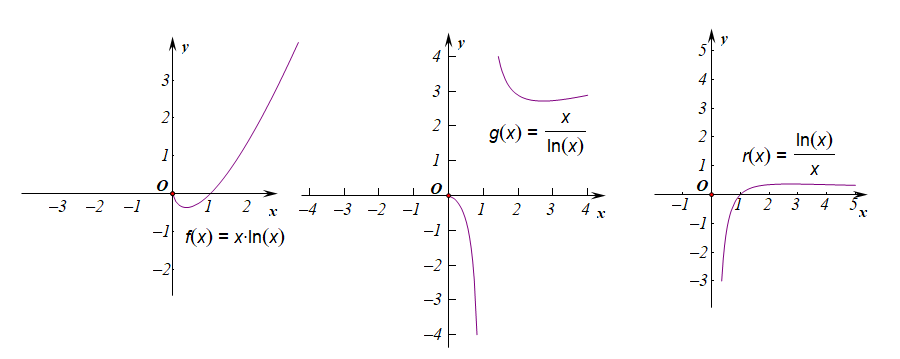
可以将他们作为导数工具的练习对象,熟练掌握他们的函数图像,有助于我们快速判断解题思路,作图时要注意因子\(e^x\)和\(\ln x\);
常用不等式
- ①、\(e^x>x+1(x\neq 0)\)
证明思路:
【法1】数形结合法,令\(f(x)=e^x\),\(g(x)=x+1\),在同一个坐标系中作出这两个函数的图像,

由图像可知,当\(x\neq 0\)时,都满足关系\(e^x>x+1\)。
补充:至于函数\(f(x)=e^x\)和函数\(g(x)=x+1\)为什么会相切与点\((0,1)\),
我们可以用导数方法来解答。
【法2】作差构造函数法,令\(h(x)=e^x-x-1\),则\(h'(x)=e^x-1\) ,
当\(x<0\)时,\(h'(x)<0\);当\(x>0\)时,\(h'(x)>0\);
即函数\(h(x)\)在\((-\infty,0)\)上单调递减,在\((0,+\infty)\)上单调递增,
故函数\(h(x)_{min}=h(0)=0\),故\(h(x)\ge 0\),当且仅当\(x=0\)时取到等号,
故\(x\neq 0\)时,总有\(h(x)>0\),即\(e^x>x+1\)。
- ②、\(e^x\geqslant x+1\),注意没有\(x\neq 0\)的条件限制。
- ③、\(\ln x\leq x-1(x>0)\)
证明思路:【法1】数形结合法,令\(f(x)=\ln x\),\(g(x)=x-1\),
在同一个坐标系中作出这两个函数的图像,
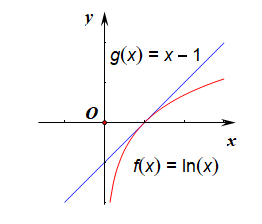
由图像可知,当\(x> 0\)时,都满足关系\(\ln x\leq x-1\)。
【法2】:作差构造函数法,令\(h(x)=\ln x-x+1(x>0)\),则\(h'(x)=\cfrac{1}{x}-1\),
当\(0<x<1\)时,\(h'(x)>0\);当\(x>1\)时,\(h'(x)<0\);
即函数\(h(x)\)在\((0,1)\)上单调递增,在\((1,+\infty)\)上单调递减,
故函数\(h(x)_{max}=h(1)=0\),故\(h(x)\leq 0\),当且仅当\(x=1\)时取到等号,
故\(x> 0\)时,总有\(h(x)\leq 0\),即\(\ln x\leq >x-1\)。
【法3】利用反函数法,此法主要基于\(e^x\ge x+1\)的结论,
由于函数\(y=e^x\)以及函数\(y=x+1\)关于直线\(y=x\)的对称函数
分别是\(y=\ln x\)和函数\(y=x-1\),故得到\(\ln x\leq x-1\)。
【法4】:利用代数变换,由\(e^x\ge x+1\),两边取自然对数得到\(lne^x\ge ln(x+1)\),
即\(x\ge ln(x+1)\),再用\(x-1\)替换\(x\),得到\(x-1\ge \ln x\),即\(\ln x\leq x-1\)。
高阶变形
\(e^x\ge x+1\)的常见变形:
比如,用\(x+1\)替换\(x\),则上式变形为\(e^{x+1}\geqslant x+2\),用\(x-1\)替换\(x\),则上式变形为\(e^{x-1}\geqslant x\),
同理可得到,\(\Rightarrow e^{x+2}\geqslant x+3\),当然,也可以得到 $\Rightarrow e^{x+n}\ge x+n+1(n\in N^*) $
当然,也可以得到 \(e^{\frac{1}{3n}}>\cfrac{1}{3n}+1(等号取不到)\)。
\(\ln x\leq x-1(x>0)\)的常见变形:
\(x+n\ge ln(x+n+1)(x\neq 1)\)
\(x-1> \ln x \xrightarrow{用\cfrac{1}{x}替换x} \cfrac{1}{x}-1> ln\cfrac{1}{x}\)
\(\Leftrightarrow \cfrac{1-x}{x}>-\ln x \Leftrightarrow \ln x>\cfrac{x-1}{x}=1-\cfrac{1}{x}\)。
\(ln\cfrac{1}{x+1}\leq \cfrac{1}{1+x}-1(x>-1) \Leftrightarrow (1+x)ln(1+x)\ge x\)
当\(x>0\)时,\(ln(x+1)<x\),故\(\cfrac{1}{x}ln(x+1)<1\),
故\(ln(x+1)^{\cfrac{1}{x}}<1=lne\),故\((x+1)^{\frac{1}{x}}<e\),
将此结论应用到自然数得到\((n+1)^{\cfrac{1}{n}}<e\),或者\((1+\cfrac{1}{n})^n<e\)。
用\(x\Rightarrow \ln x\),得到\(x\geqslant \ln x+1\).
典例剖析
(1).对于\(x\in(0,1)\),\(f'(x)>0\)恒成立,求实数\(a\)的取值范围。
分析:利用\(cosx-a>0\)在\(x\in(0,1)\)恒成立,可以求得\(a<cos1\)。
(2).当\(a=1\)时,令\(h(x)=f(x)-sinx+\ln x+1\),求\(h(x)\)的最大值。
分析:此时\(h(x)=\ln x-x+1\),如果能知道结论\(\ln x\leq x-1\),
即可知\(h(x)_{max}=h(1)=0\)。或利用导数也可以求得\(h(x)_{max}=h(1)=0\)。
(3).求证:\(ln(n+1)<1+\cfrac{1}{2}+\cfrac{1}{3}+\cdots+\cfrac{1}{n}(n\in N^*)\)。
分析:看到这样的不等式关系,我们应该想到的有裂项相消法、数学归纳法,
法1: 由(2)的结论\(\ln x \leq x-1\)得到\(ln(x+1)\leq x(x\neq 0)\),
若将其延伸到自然数,则有\(ln(n+1)<n\),再做代换,
用\(\cfrac{1}{n}\)替换\(n\),变形得到\(ln(\cfrac{1}{n}+1)<\cfrac{1}{n}\),
即\(ln(\cfrac{n+1}{n})=ln(n+1)-lnn<\cfrac{1}{n}\),
令此式中的\(n\)分别取\(1,2,3,\cdots,n\),即得到以下\(n\)个表达式:
\(ln\cfrac{2}{1}<1\);即\(ln2-ln1<1\)
\(ln\cfrac{3}{2}<\cfrac{1}{2}\);即\(ln3-ln2<\cfrac{1}{2}\);
\(ln\cfrac{4}{3}<\cfrac{1}{3}\);即\(ln4-ln3<\cfrac{1}{3}\);
\(\cdots\);\(\cdots\);
\(ln\cfrac{1+n}{n}<\cfrac{1}{n}\);即\(ln(n+1)-lnn<\cfrac{1}{n}\);以上式子累加,得到
\(ln(n+1)-ln1<1+\cfrac{1}{2}+\cfrac{1}{3}+\cdots+\cfrac{1}{n}\),
即\(ln(n+1)<1+\cfrac{1}{2}+\cfrac{1}{3}+\cdots+\cfrac{1}{n}(n\in N^*)\)。
法2:可以考虑用数学归纳法,待后思考。
证明:先用导数证明\(e^x\ge x+1\),再做代换,用\(\cfrac{1}{3^n}\)替换\(x\),
得到\(e^{\frac{1}{3^n}}>\cfrac{1}{3^n}+1\);即\(1+\cfrac{1}{3^n}<e^{\cfrac{1}{3^{n}}}\);
故\((1+\cfrac{1}{3})\cdot (1+\cfrac{1}{3^2})\cdot(1+\cfrac{1}{3^3})\cdots (1+\cfrac{1}{3^n})\)
\(<e^{\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\dots+\frac{1}{3^n}}\)
\(=e^{\cfrac{\frac{1}{3}\cdot[1-(\frac{1}{3})^n]}{1-\frac{1}{3}}}\)
\(=e^{\cfrac{1}{2}(1-\cfrac{1}{3^n})}<e^{\cfrac{1}{2}}=\sqrt{e}<\sqrt{4}=2\),
故得证。
(1).讨论 \(f(x)\) 的单调性;
分析:当 \(a \leqslant 0\) 时, \(f^{\prime}(x)<0\), \(f(x)\) 在 \((0,+\infty)\) 上单调递减,
当 \(a>0\) 时, 由 \(f^{\prime}(x)=0\) 得 \(x=\cfrac{1}{\sqrt{2a}}\),
当 \(x\in(0, \cfrac{1}{\sqrt{2a}})\) 时,\(f^{\prime}(x)<0\), \(f(x)\) 单调递减;
当 \(x \in(\cfrac{1}{\sqrt{2a}},+\infty)\) 时, \(f^{\prime}(x)>0\), \(f(x)\) 单调递增.
(2).证明: 当 \(x>1\) 时,\(g(x)>0\);
证明: 一般我们会想到求\(g(x)_{min}>0\),但是直接求最小值可能会很复杂,如果变形后估计就可能比较简单;
令 \(s(x)={e}^{x-1}-x\), 则 \(s^{\prime}(x)={e}^{x-1}-1\),
当 \(x>1\) 时, \(s^{\prime}(x)>0\), 所以 \(s(x)>s(1)\), 即 \({e}^{x-1}>x\),
从而 \(g(x)=\cfrac{1}{x}-\cfrac{e}{e^{x}}=\cfrac{e(e^{x-1}-x)}{xe^{x}}>0\);
故当 \(x>1\) 时, \(g(x)>0\).
解:原不等式等价于\(\left\{\begin{array}{l}\cfrac{a}{e^a}>0①\\\cfrac{a}{e^a}<\cfrac{1}{e}②\end{array}\right.\)
解①得到,\(a>0\),
②式化简为\(e^{a-1}>a\)③,
利用 \(y=e^{a-1}\) 和 \(y=a\) 图像可得,\(e^{a-1}\geqslant a\),
故解③式得到,\(a\neq 1\);
即原双连不等式的解集为\(a\in (0,1)\cup (1,+\infty)\);
(1)求函数 \(f(x)\) 的最大值;
解析: \(f'(x)=\cfrac{2}{x}-2x=\cfrac{2(1-x^{2})}{x}(x>0)\),
当 \(x \in(0,1)\) 时, \(f'(x)>0\), 函数 \(f(x)\) 在此区间上是增加的;
当 \(x \in(1,+\infty)\) 时, \(f'(x)<0\), 函数 \(f(x)\) 在此区间上是减少的,
所以,当 \(x=1\) 时,函数 \(f(x)\) 取得唯一极大值 \(f(1)=0\),
所以函数 \(f(x)\) 的最大值为 \(0\).
(2)证明 \(: 3+\cfrac{5}{2^{2}}+\cfrac{7}{3^{2}}+\cdots+\cfrac{2 n+1}{n^{2}}>2\ln(n+1)(n \in N^{*})\).
【证法1】: 由(1)可知,当 \(x>1\) 时, \(f(x)<0\), 即 \(2 \ln x<x^{2}-1\),
令 \(x=\cfrac{n+1}{n}(n\in N^{*})\), 则 \(2\ln\cfrac{n+1}{n}<(\cfrac{n+1}{n})^{2}-1=\cfrac{2n+1}{n^{2}}\)
即 \(\cfrac{2n+1}{n^{2}}>2\ln\cfrac{n+1}{n}\),
所以 \(3+\cfrac{5}{2^{2}}+\cfrac{7}{3^{2}}+\cdots+\cfrac{2n+1}{n^{2}}>2(\ln\cfrac{2}{1}+\ln\cfrac{3}{2}+\cdots+\ln\cfrac{n+1}{n})\),
\(=2[(\ln 2-\ln 1)+(\ln 3-\ln 2)+\cdots+(\ln (n+1)-\ln n)]=2\ln(n+1)(n\in N^{*})\)
故 \(3+\cfrac{5}{2^{2}}+\cfrac{7}{3^{2}}+\cdots+\cfrac{2n+1}{n^{2}}>2\ln(n+1)\) \((n\in N^{*})\), 证毕.
【证法2】:由常用的不等关系 \(e^x>x+1\) (\(x>0\)) 开始证明,
令\(g(x)=e^x-x-1\),则 \(g'(x)=e^x-1\),由于 \(x>0\) ,则 \(g'(x)>0\),
故函数 \(g(x)\) 在区间 \((0,+\infty)\) 上单调递增,故 \(g(x)>g(0)\),即 \(e^x>x+1\),
令 \(x=\cfrac{2n+1}{n^2}>0\) ,则 \(e^{\cfrac{2n+1}{n^2}}>\cfrac{2n+1}{n^2}+1=\cfrac{(n+1)^2}{n^2}\),
两边取自然对数得到,\(\cfrac{2n+1}{n^2}>ln\cfrac{(n+1)^2}{n^2}=2\ln(n+1)-2\ln n\)
给 \(n\)分别赋值\(n=1\),\(2\),\(3\),\(\cdots\),\(n\),得到
以上 \(n\) 个式子累加,得到
\(3+\cfrac{5}{2^{2}}+\cfrac{7}{3^{2}}+\cdots+\cfrac{2n+1}{n^{2}}>2\ln(n+1)\) \((n\in N^{*})\).
【证法3】:理科学生还可以利用数学归纳法证明;
提示:需要将选项变形后,再构造函数,\(f(x)=x+lnx\),\(g(x)=e^x-x\),答案为 \(D\);
提示:选项 \(A\) 正确,依托函数 \(y=x\cdot e^x\)来比较;选项 \(B\) 正确,依托函数 \(y=\cfrac{\ln x}{x}\)来比较;
选项 \(C\) 正确,依托函数 \(y=x\cdot \ln x\)来比较;选项 \(D\) 正确,依托函数 \(y=\cfrac{e^x}{x}\)来比较;
故选择 \(A、C、D\);
提示:对选项 \(A、B\) 做适当的变形后会发现,其实是比较函数 \(y=\cfrac{\ln x}{x}\) 与函数 \(y=\cfrac{x}{e^x}\)的大小关系;它们都可能成立;
对选项 \(C、D\) 做适当的变形后会发现,其实是比较函数 \(y=\cfrac{e^x}{x}\) 与函数 \(y=\cfrac{\ln x}{x}\)的大小关系;其中 \(D\) 不可能成立,故选 \(D\) ;
转化如下:即 \(xe^x-1\geqslant \ln x+x\)
即 \(e^{\ln x}e^x\geqslant \ln x+x+1\)
即 \(e^{\ln x+x}\geqslant \ln x+x+1\)
令 \(\ln x+x=t\),即 \(e^{t}\geqslant t+1\)
或这样转化: \(xe^x-1\geqslant x+\ln x=\ln(xe^x)\),
令 \(xe^x=t\),则 \(t-1\geqslant \ln t\)



 函数与导数中常用的函数和不等关系
函数与导数中常用的函数和不等关系
